Supervised Learning. Introduction to Neural Networks !

In my previous article on Introduction to Machine Learning, I introduced the types of Machine Learning algorithms and the different examples under each of them.

Today we are going to dive deeper into Supervised Learning and understand conceptually how Neural Networks work.

Supervised learning also known as Supervised Machine Learning is a subcategory of Machine Learning and Artificial Intelligence which is defined by it's use of labelled datasets to train algorithms that classify data or predict outcomes accurately. As input data is fed into the model, it adjusts its weights until the model has been fitted appropriately, which occurs as part of the cross validation process.

How do Neural Networks Work?

Neural Networks also known as Artificial Neural Networks (ANNs) or Simulated Neural Networks are comprised of node layers containing an input layer,one or more hidden layers and an output layer. Each node or artificial neuron, links to another and has a weight and bias attached to it. If the output of any individual artificial neuron is above the specified bias value, the neuron is activated hence sending data to the the next layer of the network. Otherwise no data is sent to the next layer. Neural networks rely on training datasets to learn and improve their accuracy with time.

Every individual node is a single linear regression model that consists of input data, weights, a bias and an output.

Mathematically we would represent it like so.

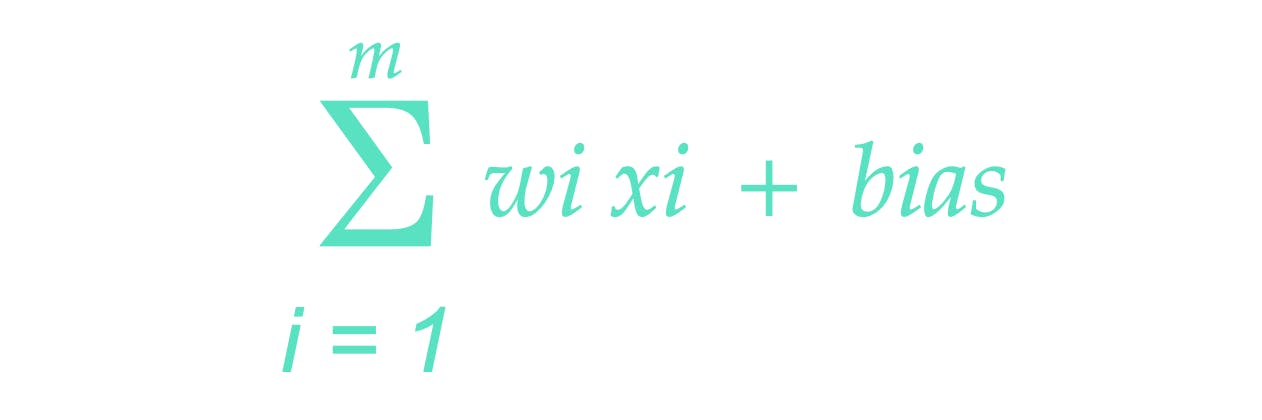
Now don't get scared by the math. Simply put, that formular is saying that all m (m is the number of input samples) inputs are multiplied by their respective weights and they are summed. The result of this summation is then added to the bias.

We also define an output function f(x) which determines whether the node passes on data to the next layer of the network

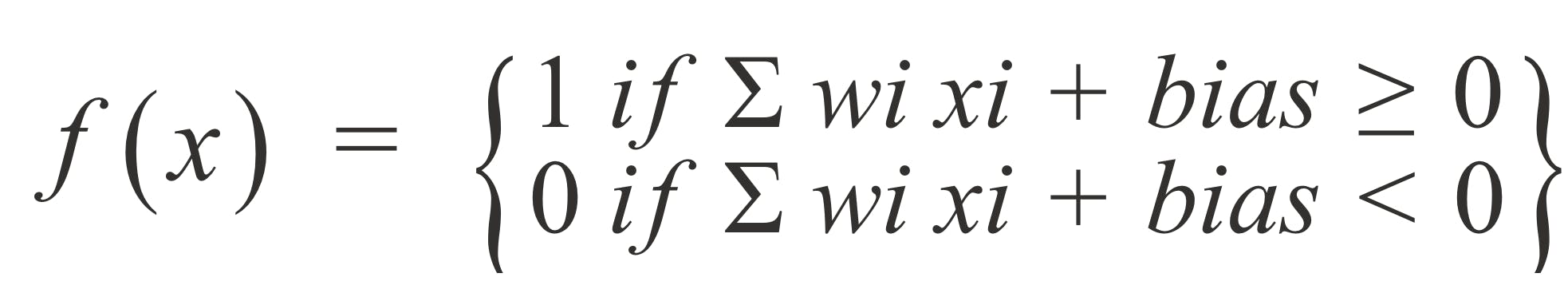
When an input layer is determined, weights are assigned. These weights help determine the level importance and relevance of any given variable. The larger one contributing more significantly to the output compared to the other inputs. All inputs are then multiplied by their respective weights and then summed.

Thereafter, the output is passed through an activation function, which determines the output. If that output exceeds a given bias, it activates the node, passing data to the next layer in the network. This makes the output of one node become the input of the next node. This process of passing data from one layer to the next layer defines the neural network as a feedward network.

To understand neural networks more and how they work, we will walk through an example and get a better understanding.

Imagine you are deciding whether to buy a new pair of shoes(Yes: 1, No: 0). The decision to buy a new pair or not will be our predicted outcome.

Assuming that there are 3 factors influencing your decision:

1. Is there enough money? (Yes:1, No: 0)
2. Are my current shoes old? (Yes:1, No: 0)
3. Do I have time to go to the mall ? (Yes:1, No:0)

Let us now assume the above giving us the following inputs:

• X1 = 0 There's not enough money to buy the shoes
• X2 = 1 Your current shoes are too ld
• X3=1 You have time to go to the mall to go get shoes

We also need to assign some weights to determine the relevance of a variable. The larger weights signify that particular variables are of greater importance to the decision or outcome

• W1 = 5 Since money is what is required to buy the shoe. It's the deal breaker
• W2 =1 Since you care about how you look. You don't want to have old shoes but it doesn't really determine whether you can get new shoes
• W3 = 1 You always have time on you but it's not really a guarantee to buy new shoes

Finally, we'll assume a bias of 3, which would translate to a bias value of -3. With all the various inputs, we can start to plug in values into the formula to get the desired output.

Y-hat = (0x5) + (1x1) + (1x1) - 3 = -1

If we use the activation function f(x) from the beginning of this article, we can determine that the output of this node would be 0, since -1 is less than 0. In this case, you wouldn't buy a new pair of shoes. But if we adjust the weights and the bias, we can get different outcomes from the model. When we observe one decision, like in the above example, we can see how a neural network could make increasingly complex decisions depending on output of previous layers.

I hope that this was insightful and hopefully you got a better understanding about what neural networks are and how they work.

In the next article we will be looking at Regression and understanding it better. Cheers